Diseño con máquinas de estados
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| Especificación | Modelado | Verificación | Implementación | Verificación | Análisis |
| PARA QUÉ | QUÉ | CÓMO | |||
| ¿Cuál es el problema? | ¿Qué tiene que hacer el sistema? | ¿El modelo cumple la especificación? | ¿Cómo hace lo que tiene que hacer? (modelo refinado) | ¿La implementación cumple la especificación? | ¿Se cumplen los plazos en el caso peor? |
| LTL, CTL | FSM / xFSM | nuXmv | fsm.h / fsm.c | nuXmv | Análisis del tiempo |
| (model checking) | Ejecutivo cíclico / FreeRTOS / Reactor | (model checking) | de respuesta |
Para empezar...
Leer [Lee&Seshia] capítulo 3. Gran parte de esta página es traducción directa de ese capítulo.
Entiende los detalles
Revisar implementación propuesta para FSM en C (fsm.h, fsm.c, fsm_ejemplo_1.c).
Estudia un ejemplo completo
Revisa un ejemplo mínimo de proyecto con ESP32 fsm-button y ESP-IDF.
Sistemas discretos
Un sistema discreto opera en una secuencia de pasos discretos y por ello se dice que tiene semántica discreta. Las entradas del sistema se modelan como eventos discretos, que son aquellos que ocurren en un determinado instante de tiempo en lugar de a lo largo del tiempo. Las entradas y las salidas se modelan como señales que indican si está presente (hay evento en ese instante) o ausente (no hay evento en ese instante).
| Señales discretas puras | Señales discretas impuras |
|---|---|
| Solo puede estar presente (hay evento) o ausente (no hay evento). | Cuando está presente (hay evento) además hay información (en este caso entero). |
Estado de un sistema
Intuitivamente, el estado de un sistema es su condición en un momento determinado. En general, el estado afecta a la forma en que el sistema reacciona a las entradas. Formalmente, definimos el estado como una codificación de todo lo que tiene que ver con el pasado y que afecta a la reacción del sistema ante las entradas actuales o futuras. El estado es un resumen del pasado.
Cuándo añadir un estado?
El estado es un resumen del pasado que tiene efecto en las reacciones del sistema. Si no hay otra forma de reaccionar, no hay necesidad de otro estado.
Máquinas de estados finitos
Una máquina de estados es un modelo de un sistema con dinámica discreta que en cada reacción hace corresponder evaluaciones de las entradas a evaluaciones de las salidas, donde la correspondencia puede depender de su estado actual. Una máquina de estados finitos (FSM) es una máquina de estados donde el conjunto de estados posibles es finito.
Si el número de estados es razonablemente pequeño, las FSM pueden dibujarse utilizando una notación gráfica. Cada estado se representa por una burbuja. Al principio de cada secuencia de reacciones, hay un estado inicial, indicado en el diagrama por una flecha colgante hacia él.
Transiciones
Las transiciones entre estados dictan la dinámica discreta de la máquina de estados y la correspondencia de las evaluaciones de las entradas con las evaluaciones de las salidas. Una transición se representa como una flecha que va de un estado a otro. Una transición también puede empezar y terminar en el mismo estado. En este caso, la transición se denomina auto-transición.
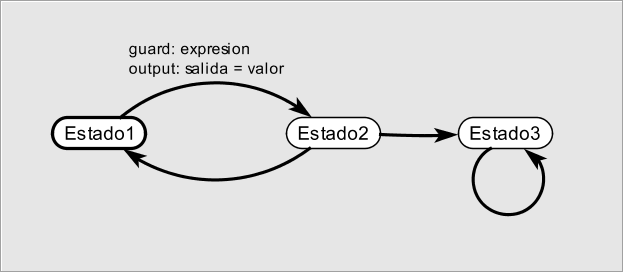 Figura: FSM de 3 estados
Figura: FSM de 3 estados
En la figura, la transición del Estado1 al Estado2 está etiquetada con guarda / acción. La guarda determina si la transición puede ser tomada en una reacción. La acción especifica qué salidas se producen en cada reacción. Una guarda es un predicado (una expresión de valor booleano) que se evalúa como verdadero cuando la transición debe tomarse, cambiando del estado origen de la transición al destino. Cuando una guarda se evalúa como verdadera, decimos que la transición está habilitada. Una acción es una asignación de valores (o ausencias) a los puertos de salida. Cualquier acción no mencionada, incluso si no se menciona ninguna acción, se considera ausente implícitamente.
Éste podría ser un modelo de FSM para el contador de coches en la puerta de un aparcamiento público. Un detector de entrada (up) detecta cuando entra un nuevo coche y otro (down) detecta cuando sale un nuevo coche. Es un ejemplo de cómo una máquina de estados de un sistema aparentemente sencillo puede complicarse considerablemente. De hecho una máquina de estados no puede modelar cualquier sistema computable, no es Turing-complete. ¿Qué pasaría si la guarda del estado 0 al 1 fuera simplemente up?
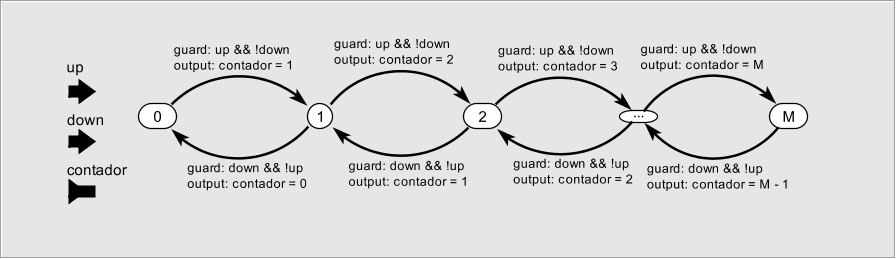 Figura: Contador del garaje
Figura: Contador del garaje
Las guardas pueden ser relativamente complejas, incluyendo condiciones sobre entradas impuras que modelan datos proveniente de sensores. Por ejemplo, el termostato de una caldera:
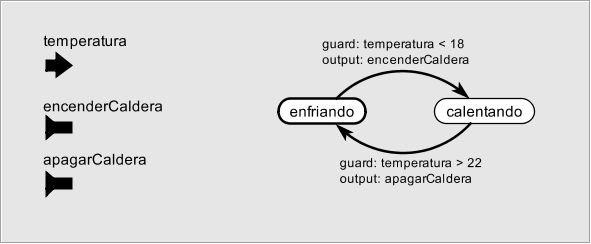 Figura: Control de caldera
Figura: Control de caldera
La FSM especifica completamente el sistema
Nuestra descripción informal del contador del garaje no indica explícitamente lo que ocurriría si la cuenta estaba en 0 y un coche sale. Una gran ventaja de los modelos FSM es que definen todos los comportamientos posibles. La FSM define lo que ocurre en esta circunstancia. El recuento se mantiene en 0. En consecuencia, las FSM se prestan a la comprobación formal, que determina si los comportamientos especificados son de hecho comportamientos deseables.
Se puede indicar explícitamente una transición por defecto como en la figura. Suele representarse con línea punteada. Solo se aplica si no hay otra transición activa.
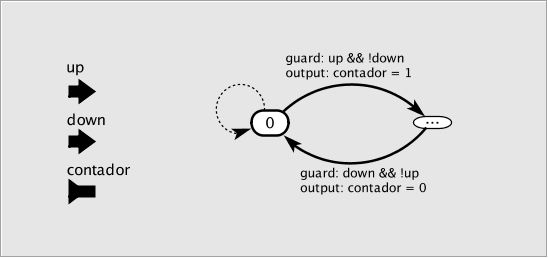 Figura: Ejemplo de transición por defecto
Figura: Ejemplo de transición por defecto
Función de actualización
Una máquina de estados se define por los siguientes elementos:
- Un conjunto de estados . La máquina siempre tiene un único estado actual. Al empezar la máquina se encuentra en el estado inicial .
- Un conjunto de entradas . Las entradas comunican la máquina con el entorno. Pueden ser sensores de magnitudes físicas (temperatura, presión, humedad, velocidad, aceleración, etc.) o contadores, o temporizadores.
- Un conjunto de salidas o acciones . Las acciones permiten reaccionar ante los cambios en el entorno provocando otros cambios en el entorno. Pueden activar actuadores, o iniciar temporizadores, o comunicar valores a otras máquinas de estado.
- Una función de actualización . Si está definida en el momento de la reacción, esta función determina el siguiente estado y las reacciones (salidas).
Los diferentes tipos de máquinas de estado se diferencian en cuándo se actualiza el estado actual y las acciones, en las características de la actualización (puede no ser función) y en su relación con otras máquinas de estado que se ejecutan sobre el mismo entorno.
Si el momento en el que se disparan las transiciones es ante la ocurrencia de algún evento significativo (cambio en entradas) entonces se dice que la máquina es disparada por eventos. Si el momento en que se disparan las transiciones es de forma periódica se dice que es disparada por tiempo. Este último tipo es el que va a ser objeto de estudio durante este curso.
Maquinas de Mealy y máquinas de Moore
En este curso nos centraremos en las máquinas de estados finitos que hemos visto, que se denominan Máquinas de Mealy. Existe otra variante en la que la generación de las salidas no depende de las entradas, sino solo del estado actual, denominadas Máquinas de Moore, muy utilizadas en la síntesis de circuitos digitales.
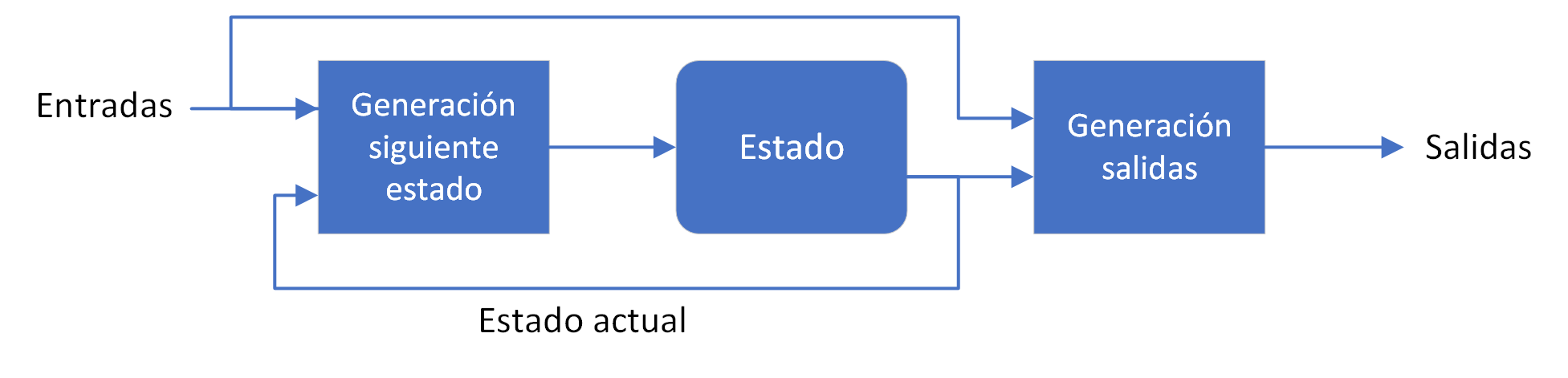 Figura: Diagrama de una máquina de Mealy
Figura: Diagrama de una máquina de Mealy
Las máquinas de Mealy tienden a ser más compactas que sus equivalentes máquinas de Moore. Es posible transformar una máquina de Moore en una máquina de Mealy y viceversa. Sin embargo la transformación de Mealy a Moore provoca que la máquina reacciona (produce salidas) un ciclo después. El motivo es simple, la actualización del estado es la que provoca el cambio en las salidas. Por tanto, no puede cambiar el estado y las salidas a la vez.
Desarrollo de la metodología
Una vez construido el modelo, normalmente de forma gráfica, la metodología nos lleva a dos pasos de verificación. Por un lado especificaremos la máquina de estados y el entorno usando un lenguaje de verificación formal (SMV). Por otro lado refinaremos el modelo realizando una implementación en C. La implementación no tiene por qué coincidir exactamente con el modelo inicial, así que volveremos a especificar la máquina correspondiente al programa en SMV, para verificarla nuevamente. Finalmente, procederemos a realizar un análisis de planificabilidad para garantizar que se cumplirán los plazos de ejecución.
Un ejemplo muy sencillo
Veamos cómo modelar la máquina de estados que controla la luz de un portal. La luz tiene dos posibles estados, apagada y encendida. Inicialmente parte del estado apagado, que denominaremos estado 0. Al recibir un evento de pulsación de cualquier interruptor la luz pasa al estado encendido, estado 1, se enciende y da comienzo la cuenta atrás de un temporizador durante un número de segundos. Al expirar el temporizador la luz pasa a estado apagado. Veamos gráficamente:
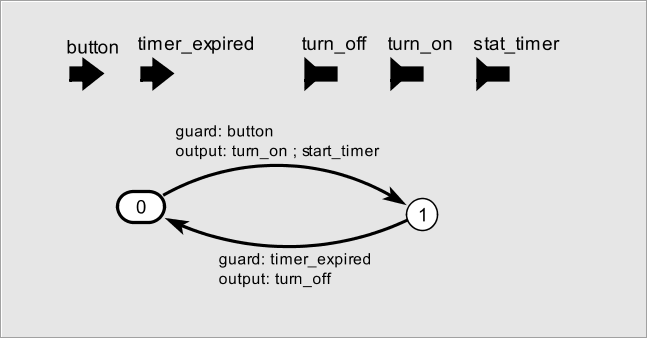 Figura: Control de luz en portal
Figura: Control de luz en portal
El temporizador y los pulsadores no pertenecen al sistema que queremos comprobar, así que entran a formar parte del entorno. A la hora de verificar tendremos que proporcionar también un modelo del entorno.
Implementación en C
Para implementar máquinas de estado se propone un sencillo módulo en C.
Empezaremos describiendo la interfaz pública, descrita en el archivo fsm.h:
fsm.h1#ifndef FSM_H 2#define FSM_H 3 4typedef struct fsm_t fsm_t; 5 6typedef int (*fsm_input_func_t) (fsm_t*); 7typedef void (*fsm_output_func_t) (fsm_t*); 8 9typedef struct fsm_trans_t { 10 int orig_state; 11 fsm_input_func_t in; 12 int dest_state; 13 fsm_output_func_t out; 14} fsm_trans_t; 15 16struct fsm_t { 17 int current_state; 18 fsm_trans_t* tt; 19}; 20 21fsm_t* fsm_new (fsm_trans_t* tt); 22void fsm_init (fsm_t* this, fsm_trans_t* tt); 23void fsm_update (fsm_t* this); 24 25#endif
Respecto a la definición del principio se han tomado algunas decisiones de diseño que impone restricciones adicionales al modelo:
-
Se asume que el estado inicial es el estado origen de la primera transición en la tabla de transiciones. Es una limitación que no resta generalidad al modelo, porque de hecho es habitual describir la tabla de transiciones desde el estado original.
-
Se recorre la tabla de transiciones en orden y se aplica la primera transición que cumple la condición de disparo (estado origen igual al estado actual y función de entrada activa).
Sin embargo, no se imponen otras restricciones a la función de actualización del estado actual, ni al momento en que se ejecuta. Como veremos, esto permite modelar máquinas de estados disparadas por eventos o por tiempo, jerárquicas, con modelos de concurrencia asícrono o síncrono, etc.
Volvamos entonces a la implementación del ejemplo. Una forma sencilla de abordar el problema es tratar primero con la interacción con el entorno. Ésta sería una versión para simulación. La versión para ejecución debe tratar con periféricos del microcontrolador para entradas/salidas digitales y para temporizadores.
environment.h1#ifndef ENVIRONMENT_H 2#define ENVIRONMENT_H 3 4int button_pressed(void); 5void button_set(int value); 6 7int timer_expired(void); 8void timer_start(void); 9void timer_next(void); 10 11#endif
El temporizador podría ser una máquina de estados extendida, pero ya lo veremos más adelante. La aplicación principal es sumamente sencilla.
main.c1#include <stdlib.h> 2#include "fsm.h" 3#include "environment.h" 4 5// salidas 6 7void lampara_on (fsm_t* fsm) 8{ 9 printf("[t=%d] lampara -> ON\\n", t); 10 timer_start(); 11} 12 13void lampara_off (fsm_t* fsm) 14{ 15 printf("[t=%d] lampara -> OFF\\n", t); 16} 17 18// constructor 19 20fsm_t* lampara_new (void) 21{ 22 static fsm_trans_t lampara_tt[] = { 23 { 0, button_pressed, 1, lampara_on }, 24 { 1, button_pressed, 1, lampara_on }, 25 { 1, timer_expired, 0, lampara_off }, 26 { -1, NULL, -1, NULL }, 27 }; 28 return fsm_new (lampara_tt); 29} 30 31// casos de simulación 32 33void simulate_environment(int t) 34{ 35 button_set(t >= 50 && t < 53); 36} 37 38// programa principal 39 40int main() 41{ 42 fsm_t* lampara_fsm = lampara_new(); 43 for (t = 0; t < 1000; ++t) { 44 fsm_update (lampara_fsm); 45 simulate_environment(t); 46 timer_next(); 47 } 48}