Máquinas de estados extendidas
| 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| Especificación | Modelado | Verificación | Implementación | Verificación | Análisis |
| PARA QUÉ | QUÉ | CÓMO | |||
| ¿Cuál es el problema? | ¿Qué tiene que hacer el sistema? | ¿El modelo cumple la especificación? | ¿Cómo hace lo que tiene que hacer? (modelo refinado) | ¿La implementación cumple la especificación? | ¿Se cumplen los plazos en el caso peor? |
| LTL, CTL | FSM / xFSM | nuXmv | fsm.h / fsm.c | nuXmv | Análisis del tiempo |
| (model checking) | Ejecutivo cíclico / FreeRTOS / Reactor | (model checking) | de respuesta |
Para empezar...
Leer [Lee&Seshia] capítulo 3. Gran parte de esta página es traducción directa de ese capítulo.
Practica
Hacer la práctica planteada en Campus Virtual.
FSM deterministas y receptivas
Una máquina de estados es determinista cuando para cada estado existe como mucho una transición activa por cada valor de entrada posible. La definición formal de un FSM dada en el tema anterior garantiza que es determinista, ya que la actualización es una función, no un mapeo de uno a muchos. Sin embargo, la notación gráfica con guardias en las transiciones no tiene esta restricción. Una máquina de estados de este tipo sólo será determinista si las guardas que salen de cada estado no se solapan.
Una máquina de estados determinista es determinada, lo que significa que dadas las mismas entradas siempre producirá las mismas salidas. Sin embargo, no todas las máquinas de estado determinadas son deterministas. Por ejemplo, nuestra implementación de FSM es siempre determinada porque recorre la tabla de transiciones en orden y aplica solo la primera activa, pero permite especificar máquinas no deterministas. ¿Qué habría que cambiar para que no sea determinada? ¿Qué ventajas e inconvenientes presentaría?
Una máquina de estados es receptiva si, para cada estado, hay al menos una transición posible en cada símbolo de entrada. En otras palabras, la receptividad garantiza que una máquina de estado esté siempre preparada para reaccionar a cualquier entrada y no se quede atascada en ningún estado. La definición formal de un FSM dada anteriormente garantiza que es receptiva, ya que la actualización es una función, no una función parcial. Está definida para todos los estados y valores de entrada posibles. Además, en nuestra notación gráfica, como tenemos transiciones implícitas por defecto, nos hemos asegurado de que todas las máquinas de estado especificadas en nuestra notación gráfica son también receptivas.
Máquinas de estados extendidas
Recordemos el ejemplo de máquina de estados para contar los coches que hay en un aparcamiento público. La representación completa para un caso real es completamente inmanejable. Este problema aparece frecuentemente al modelar con máquinas de estados. Es muy fácil que el número de estados crezca más allá de lo manejable por una persona.
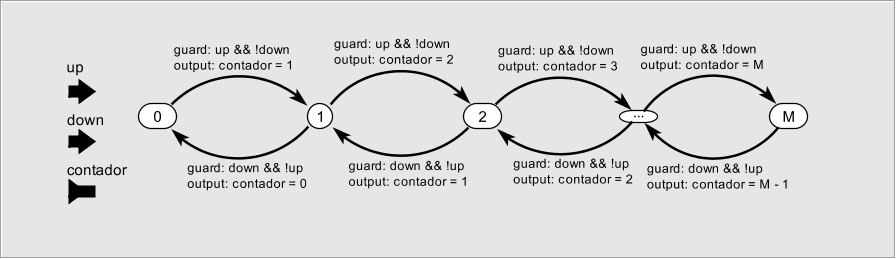 Figura: Contador del garaje
Figura: Contador del garaje
Para resolver este problema se desarrollaron las máquinas de estados extendidas. Se amplía el modelo con variables que pueden ser leídas y escritas en las funciones de entrada y salida. Veamos cómo se simplifica la máquina de estados anterior.
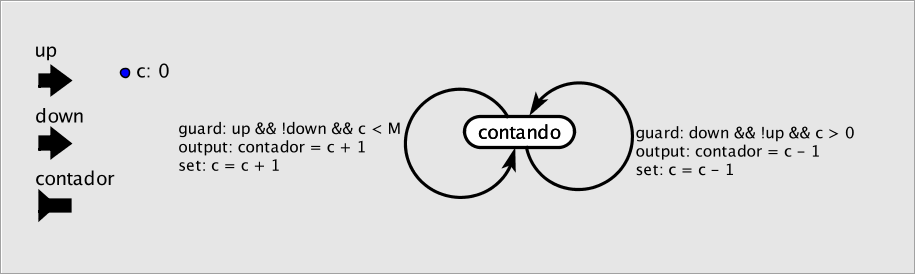 Figura: Contador del garaje
Figura: Contador del garaje
El estado de una máquina extendida no es solo el valor del estado, sino también el de todas las variables. Esto implica que no hemos reducido el espacio de estados sino que simplemente hemos compactado su representación.
Detalles de implementación
La implementación en C de una máquina extendida puede realizarse también con la biblioteca propuesta en el tema anterior. En este caso la máquina de estado debe enriquecerse con las variables, por lo que una posibilidad es incluir los datos en la propia estructura que modela la máquina de estados. En los lenguajes orientados a objeto esto se hace mediante herencia, pero C no es orientado a objetos, por lo que tendremos que implementar algo parecido a la herencia. Vamos a ilustrarlo con el ejemplo del contador del aparcamiento.
parking.c1#include "fsm.h" 2 3typedef struct { 4 fsm_t parent; 5 int c, M; 6} parking_fsm_t; 7 8int entra_coche(fsm_t* fsm) 9{ 10 parking_fsm_t* this = (parking_fsm_t*) fsm; 11 return up() && !down() && this->c < this->M; 12} 13 14int sale_coche(fsm_t* fsm) 15{ 16 parking_fsm_t* this = (parking_fsm_t*) fsm; 17 return down() && !up() && this->c > 0; 18} 19 20void inc_coches(fsm_t* fsm) 21{ 22 parking_fsm_t* this = (parking_fsm_t*) fsm; 23 ++this->c; 24} 25 26void dec_coches(fsm_t* fsm) 27{ 28 parking_fsm_t* this = (parking_fsm_t*) fsm; 29 --this->c; 30} 31 32fsm_t* parking_fsm_new(int M) 33{ 34 static fsm_trans_t parking_tt[] = { 35 { 0, entra_coche, 0, inc_coches }, 36 { 0, sale_coche, 0, dec_coches }, 37 { -1, NULL, -1, NULL }, 38 }; 39 parking_fsm_t* self = (parking_fsm_t*)malloc(sizeof(parking_fsm_t)); 40 fsm_init(&self->parent, parking_tt); 41 self->c = 0; 42 return &self->parent; 43}
Máquinas extendidas en ESP32
Paso a paso
Utilizaremos el entorno ESP-IDF que no es más que una adaptación de FreeRTOS proporcionada por el propio fabricante con bibliotecas adicionales para soportar todos los periféricos del ESP32. Visita la página de Software para instrucciones de instalación.
El código completo de este ejemplo puede obtenerse en este enlace. El ejemplo a implementar es el de la luz de un portal:
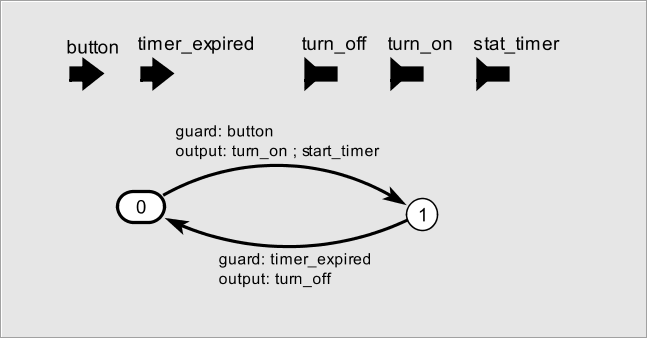 Figura: Control de luz en portal
Figura: Control de luz en portal
Entra en ESP-IDF pinchando en el símbolo de Espressif en Visual Studio Code, crea un nuevo proyecto. Elige tu modelo de placa (si no lo conoces elige ESP32 chip via ESP-PROG). El programa automáticamente generado está vacío pero ya puede compilarse, simplemente pinchando en el icono con el símbolo
Respecto a lo visto en el capítulo anterior solo tenemos que proporcionar un modo de interactuar realmente con el entorno y temporizar correctamente cada uno de los ciclos de la máquina de estados. En este curso nos centraremos en máquinas de estado disparadas por tiempo, también llamadas máquinas síncronas, aunque el término síncrono se emplea para referirse también a la semántica de concurrencia cuando hay más de una máquina de estados.
El bucle principal del programa es siempre igual:
main.c1#include <freertos/FreeRTOS.h> 2#include <freertos/task.h> 3// ... 4void app_main() 5{ 6 // ... 7 TickType_t last = xTaskGetTickCount(); 8 for (;;) { 9 fsm_update (fsm); 10 vTaskDelayUntil(&last, pdMS_TO_TICKS(FSM_CYCLE_PERIOD_MS)); 11 } 12}
La función xTaskGetTickCount devuelve el reloj lógico del sistema operativo (FreeRTOS). Es un número creciente que cambia a un ritmo constante. La función vTaskDelayUntil duerme la tarea durante un tiempo tal que entre la marca horaria last (que se pasa como puntero) y el momento de despertar pase el tiempo lógico indicado como segundo argumento. El tiempo lógico de cada periodo se puede obtener a partir del tiempo físico con la función pdMS_TO_TICKS. La marca horaria last corresponde al reloj lógico en el momento de la última llamada a xTaskGetTickCount o a vTaskDelayUntil.
En sistemas reales solo existirá ese bucle y, como mucho, podrá haber más llamadas a funciones fsm_update para otras máquinas de estado. Sin embargo, todavía no hemos visto la composición de máquinas de estado, así que tendremos que ejecutar también la función ad-hoc que hemos hecho para decrementar el temporizador (timer_next).
La interacción con el entorno se puede hacer de muchar formas, pero vamos a mostrarla de la forma más simple posible. El módulo GPIO (General Purpose Input/Output) proporciona funciones para acceder a las entradas y salidas digitales. En la función app_main primero configuramos los pines como corresponda:
1gpio_reset_pin(LED); 2gpio_reset_pin(BUTTON); 3gpio_set_direction(LED, GPIO_MODE_OUTPUT); 4gpio_set_direction(BUTTON, GPIO_MODE_INPUT); 5gpio_set_pull_mode(BUTTON, GPIO_PULLUP_ONLY);
El pin LED se configura como salida (GPIO_MODE_OUTPUT) y el pin BUTTON como entrada (GPIO_MODE_INPUT). En el pin BUTTON habilitamos una resistencia de pull-up que pone la tensión de entrada en un valor alto cuando no hay nada conectado. Sin embargo, al cerrar el interruptor, conectaremos la pata de entrada con la masa. Es decir, el valor que devuelve gpio_get_level por defecto es 1, y cuando se pulsa el botón es 0. O dicho de otro modo, es una entrada activa a nivel bajo. Por eso en el ejemplo definimos la constante BUTTON_LEVEL_ACTIVE con el valor 0, indicando qué valor debe tener la entrada para considerar que ha ocurrido el evento:
1int button_pressed() 2{ 3 return BUTTON_LEVEL_ACTIVE == gpio_get_level(BUTTON); 4}
Hay un motivo para usar esta lógica inversa, que tiene que ver con limitar la corriente máxima que puede circular por el transistor de entrada, de manera que no se queme el transistor de entrada. Por supuesto, se puede usar una entrada activa a nivel alto, pero entonces se debería incluir una resistencia para limitar la corriente máxima y no quemar el transistor de entrada.
Variables de la máquina extendida
Las variables de una máquina extendida podrían almacenarse en globales, pero eso resultaría muy poco conveniente si necesitamos varias instancias de una misma máquina extendida. En general lo más probable es que nos interese tener nuestro propio tipo abstracto de datos (TAD). Para poder usar la biblioteca fsm.h y fsm.c debemos asegurarnos de que el primer campo de nuestro TAD es un fsm_t. En ese caso los punteros a nuestro TAD serán también punteros a una fsm_t. De hecho, será tan frecuente usarlos como punteros a fsm_t que probablemente no nos interesa devolver un puntero a nuestro TAD en el constructor. Vamos a ilustrarlo con un ejemplo, ambas implementaciones son equivalentes.
1typedef struct { 2 fsm_t parent; 3 int c; 4} parking_fsm_t; 5 6fsm_t* parking_fsm_new() { 7 static fsm_trans_t tt[] = { 8 {0, entra_y_no_sale, 0, inc_coches}, 9 {0, sale_y_no_entra, 0, dec_coches}, 10 {-1, NULL, -1, NULL}, 11 }; 12 parking_fsm_t* self = (parking_fsm_t*) 13 malloc(sizeof(parking_fsm_t)); 14 fsm_init(&self->parent, tt); 15 self->c = 0; 16 return &self->parent; 17}
Ambos estilos son equivalentes pero a la hora de usarlos suele ser más conveniente el de la izquierda, y por eso es el que vamos a usar:
1void app_main() { 2 fsm_t* p = parking_fsm_new(); 3 for(;;) { 4 fsm_update(p); 5 // ... 6 } 7}
Acceder a las variables de la máquina extendida
Las funciones de entrada y salida de la máquina de estado aceptan un fsm_t* como primer argumento. En las máquinas extendidas sabemos que ese fsm_t* es también un puntero a la máquina extendida. Por tanto para acceder a los campos no hay más que hacer una operación de moldeo (cast):
1void inc_coches(fsm_t* fsm) 2{ 3 parking_fsm_t* self = (parking_fsm_t*) fsm; 4 ++self->c; 5}
Esa operación de moldeo puede resultar inconveniente a veces, así que es posible utilizar una función intermedia que lo hace:
1void parking_fsm(fsm_t* fsm) { return (parking_fsm_t*) fsm; }
Con esta función acceder a las variables de la máquina extendida puede ser más natural:
1void inc_coches(fsm_t* fsm) { ++parking_fsm(fsm)->c; }
Si lo que te preocupa de este método es la eficiencia del resultado mira en otro lado, porque cuando compiles en modo release probablemente desaparecerá todo rastro de la función parking_fsm en el binario generado.
Errores frecuentes
-
Una función de entrada no debe tener efectos de lado de ningún tipo. No puede haber asignaciones a ninguna variable de estado en la función de entrada.
-
En la implementación en C una función de salida puede y debe actualizar también las variables de la máquina extendida. No actualices variables de la máquina extendida fuera de las funciones de salida.
-
Todas las variables auxiliares para la máquina extendida forman parte del tipo de datos de la máquina extendida. No uses variables globales para almacenar datos propios de la máquina de estados. A lo mejor ahora no tienes problemas, pero los tendrás si la máquina se utiliza en una composición concurrente o jerárquica.